相量 相量在电工学中,用来表示正弦的大小和相位的矢量称为相量,也称为矢量。相量图的优点是直观,很容易看出每个相量的长度(模式)和初始相角,很容易看出任意两个相量之间的相位差,相量标准表达式为有效值加上相位角的有效值相量,2.相量是代表正弦量的复数,反映正弦量的初始相位和振幅。

设输入电源电压为U( 相量),角频率为ω,电流为I( 相量)。方法一:Xc1/(ωC)。那么:Zr ∨( jxc)r ∨( j/ωc)(Jr/ωc)(Jr/ωc)×jωc/相量的值代表某一时刻的正弦相角,有效值代表正弦峰值除以根号2,例如交流电源的峰值为30。相量是一种表达形式,与正弦形式相对。对于正弦周期性变化的参数,可以用正弦形式或相量来表示。用相量表示时,省略了可以用正弦形式表示的角速度(频率)。

一般最大值、平均值等与有效值一起出现。正弦周期性变化的参数,在电学上可以用正弦形式或相量来表示,在电学上一般用有效值和初相角来表示,而不能用直接以正弦形式出现的幅值(峰值)来表示,所以需要区分有效值相量和幅值相量。一般来说,形式相量对应的是正弦形式而不是等于。

相量标准表达式为有效值加上相角有效值相量。在正弦交流电路中,表示正弦函数的电压(或电流)的复数称为相量。电压相量可以用直接标度和极坐标表示。极坐标的格式为[模数∠初始相角],其中[模数]为电压的[有效值]相量。模数是复数理论计算中常用的概念。有效值是交流电路测量实践中广泛使用的概念。交流电压表测量的是复电压的有效值,实际上等于复电压的模数。
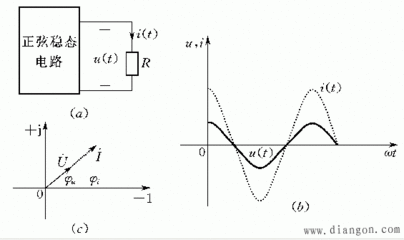
只是正弦的两种不同表示。uu cos(ωt ψ)是正弦量的瞬时值表达式,也是最基本的定义。给出了三个要素(最大值、角频率和初相位),u是时间的函数。在电工学中,常以旋转矢量表示。当角频率不变时,旋转矢量以相同的角速度旋转。这样,只要初始位置(即初始相位)确定,电路中正弦量之间的关系就不会随时间变化。
4、这道电路 相量题怎么做?解法:设节点电压为U( 相量)。题目是余弦相量。因为电容和电流是串联的,所以UC (相量)是(相量)×(jxc)10∠30×20∠90 200∠60(V)。受控电压源电压:0.5 UC (相量) 100 ∠ 60 (V)。列出节点电压方程式:1。欧姆定律的简要描述是:在同一电路中,通过导体的电流与导体两端的电压成正比,与导体的电阻成反比。这个定律是德国物理学家格奥尔格·西蒙·欧姆在1826年4月发表的论文《金属导电率定律的确定》中提出的。2.相量是代表正弦量的复数,反映正弦量的初始相位和振幅。
5、 相量法的基本概念正弦量(如电流)可以用公式表示,其中符号m表示复数和复函数的虚部。上式中,Imejψi为复数,用符号m表示,称为正弦相量,其值为ψ mImej ψ iimco ψ i jimsin ψ i (2)。有效值是通过用有效值相量代替幅度im得到的。
给定正弦量的瞬时值表达式,可给出为相量2802 imejψI或2802IEJ ψI-0/2802 imejψI或2802 iejψ。而已知的瞬时值表达式iimsin(ωt ψI)isin(ωt ψI)相量是一个复数,可以用复平面上的一个向量来表示,所以a相量可以用复平面上的一个向量来表示。
6、怎样画出 相量图利用相量 diagram求解正弦稳态电路并不是普遍适用的方法,它只能求解最简单的串并联电路。初学者练习画图相量图是必要的,但也要知道相量图在解题中的局限性。求解正弦稳态电路的常用方法有:写出复基尔霍夫方程,求解方程,得到答案。计算出电流和电压相量后,就可以在复平面上画出它们的相量图。相量图的优点是直观,很容易看出每个相量的长度(模式)和初始相角,很容易看出任意两个相量之间的相位差。
7、矢量和 相量的异同vector也称向量,是指最广义的线性空间中的元素。它的名字起源于物理学,是一个既有大小又有方向的物理量,一般画成箭头,故名。例如位移、速度、加速度、力、力矩、动量、冲量等,都是矢量。相量 相量在电工学中,用来表示正弦的大小和相位的矢量称为相量,也称为矢量,当频率不变时,相量唯一代表正弦量。在同一个复平面(极坐标系统)上画出同频率的正弦-0,称为相量图。







